乳状液的聚结

聚结的结果是什么呢?很显然,当液滴聚集在体系的顶部或底部时，它们被迫接触而结合。如果液滴在流体中运动时产生碰撞，也可以聚结。液滴是如何碰撞的呢？两个被布朗运动推动的液滴可以碰撞。这种现象多发生在较小的液滴之间，就像我们所演示的较小的液滴运动有较大的随意性。小液滴可以和大液滴碰撞。快速下落的较大的液滴可以带动较慢的液滴。液滴可以撞击，润湿容器的内壁，于是其它的撞击内壁的液滴可以在内壁上同液体薄膜聚结，所有产生了这些结果的同时，某些反应可以发生。
考虑第一种情况，两液滴每次碰撞都可聚结，这可能是一种纯液体分散到另一种与之不相混溶、不反应的纯液体中的情况。现在，假定液滴与四壁是弹性碰撞，又假定是在最简单的情况下--液滴不带电。没有大范围的引力在做功。甚至这最简单的情况也会产生许多结果。在对它的规律做具体的数学分析尝试或甚至粗略的近似之前。最好有一个总的看法。
由于每个极小的液滴都在围绕一个缓慢下降的质点做随意运动。大液滴沿近似直线较快的下降。可以把水液滴的轨迹描绘成模糊的小球，而把大的液滴描绘成一个和液滴具有相当直径的圆柱体。中间尺寸的液滴则可这样描述，它就像描述近似螺旋形圆柱体一样，大的一端具有近似水平的取代物，其直径近似于液滴直径，小的一端则比较斜且具有模糊的界线。无论何时，两个或多个液滴的轨迹在空间和时间上重叠，则发生聚结。新的液滴的体积将具有两个原来液滴体积之和，但直径不是原来两个液滴的直径之和。所有的条件都是显而易见的，但需要在估算结果前分别考虑。另一个因素，像分散相的浓度，对聚结速度有很大的影响。我们已讨论液滴在空间聚集的结果。当液滴的平均空间比平均轨迹的有效半径小时。液滴的接触就成为必然。然而，当液滴聚结时，其平均半径会增大。随液滴总数的减少，液滴的碰撞机会也在减少，还有几个简单的因素。它们可以加和成为一个复杂的、不确定的情况。smoluchowski-muller方程对聚结速度有两个定量关系：作用半径和有效碰撞，应用这两个定量去解各个未知方面。我们能使一些实验数据相符，但不能精确地预测我们遇到的下一个问题将会出现什么情况。这在实际应用领域的破乳作用的情况下是一个真正的困难。最好的方法是注意所有起作用的因素，决定哪一个是主要因素，再进行测试去解决最后问题。

假定两个液滴相互接近，将会涉及什么因素呢？如果液滴带有电荷。将会有电场效应。当液滴非常密，将开始加以考虑引力。如果两液滴在液体中下落，一个低压区将在它们之间产生，把它们拉到一起，这些和别的影响可以在一定条件下发生作用。这些暗示着在许多领域的问题都是这样的。有如此多的不确定因素，以至于一个严格的可以以全部预测事件的方程也是不可能的。这是否意味着我们应当对理论方法失去信心呢?当然不是，系统的研究和描述每一个因素是完全可能的，并且每一步都有使我们离全面理解它都更近了。

现在考虑两个液滴又是如何聚结的。很显然。一个大液滴具有比两个各为其一半体积的小液滴更小的表面积，如果要在界面面积上做功，系统将趋于最小的表面积，另一方面，当表面张力接近于0时，将会有很小的拉力引起聚结。对乳状液在热力学稳定下，其表面张力一定是零。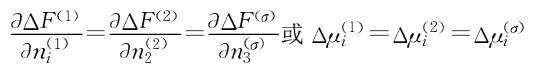
这里对ui(1)是成分i在相1中的化学势；ui(2)是成分i在相2中的化学势；ui(σ)是成分i在界面的化学势。
并且，众所周知。一种乳状液可以稳定存在一段时间。微乳液存在热力学平衡。一般来说，普通乳液是固有不稳定的。
因为乳状液存在几种组分，又由于存在弯曲的界面。Okazawa和Bron采取了忽略化学潜能的离子效应。这种效应在离子表面活性剂中又不得不加以考虑，但由于非离子表面活性剂能产生稳定的乳化作用，他们认为离子效应可以分离出来对待。
在一个含有具有体积为V(D)的N(D)个液滴和界面积a(D)的微乳状液滴的体系中，在温度t和外部压强P0时，假设外相体积为
V(E)。Bron指出：对系统所做的功只是P0和总体积V的函数。正是这个原因，他们才选取了hemholt自由能作为热动力学的基本函数而不是吉布斯自由能。
系统被认为是由两个液相即连续的外相和液滴所组成。其中吸附在界面的相的特征函数用上标表示。
作用在系统上的机械功现在就变成了dW=Po[dV(1) +dV(2) +dV(σ)]，这个式子表明界面相变成了由三部分组成。既然G=U-TS+ P0V，我们就得dG=一Sdt + [V(1) +V(2) +V(σ)] dPo +∑iu(1)dni(1) + ∑iu(2)dni(2) + ∑iu(σ)dni(σ)，在这个式子中ni(J)表明相J中i组分的分子数目，ui(J)表示相J中i组分的化学势。
现在我们假定温度和外压力均不变，最小的G就导致了平衡的产生，即 ui(1)=ui(2)=ui(σ)

这个条件是在忽略液滴内压和总体积，界面张力或界面积的情况下获得的。在特定的情况下，界面张力等于0；则: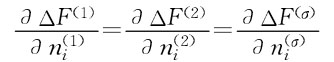
这种研究方法是在假定系统的体积变化是足够小，压缩系统数也很小可以忽略的情况下进行的。
我们怎样用特定的系统来解释这个等式呢?现在假定一个由纯净水、纯净正辛烷和纯净非离子表面活性剂所组成的系统。当这三种物质混合时，水就会变成正辛烷的水溶液，正辛烷则变成水的正辛烷饱和溶液。表面活性剂会分散于这两个液相之间。在给定的温度压力下，当化学势相等时，这个分散过程就达到了平衡，若没有表面活性剂的加入，两相之间就存有界面张力。如果这时要将一相分散于另一相中就必须克服张力做功，注意在这里每相都有可能成为外相。既然增大界面面积需要做功，那么系统就会向面积趋于最小的方向进行，并且所有的分散系统都是不稳定的。如果提供的表面活性剂是适合的，表面活性剂就会集中于两相之间的界面上。并且其亲水基和疏水基分别仲向水相和正辛烷(油相)内。这样就降低了两相之间界面张力。换句话说，由于表面活性剂的存在，才防止了液滴的聚结。